If the Earth Is A True Globe

If the Earth is a true globe – there wouldn’t be a single serious argument against the fact of the Earth’s globular shape (roundness) ….Not a single argument!

There would be no flat earth arguments as the earth would display the characteristics of a globe and flatearthers would not be able to present any arguments as to flatness or lack of globularity of the earth.

A search of the circumference of the earth on Google will show the following:

The earth is 24,901 miles ( 40,075 kilometers) around. This means if you start at the center of the equator and travel around the earth you will return to the same place and travel 24,901 miles.

Now - since the earth is presented as a globe - a ball - you should be able to break this circle into 360 degrees as all circles ( balls) can be divided into 360 parts.

Circumference of earth - 24,901 miles divided by 360 degrees equals 69.16 miles

Circumference of earth - 40,075 kilometer divided by 360 degrees equals 111.31 kilometers.

All we have done is create a division of how much space would be between each of these 360 degrees.

So - every 69.16 miles or 111.31 km we have a division which equals one degree of the total 360 degrees of a circle.

Now - lets look at a ball ( globe) and compare the distance between these two (2) points.

If we take any point on a ball and move an equal distance from that point in 4 directions we will find the first position will be the top and the other four (4) distances will be lower in orientation to the first point.

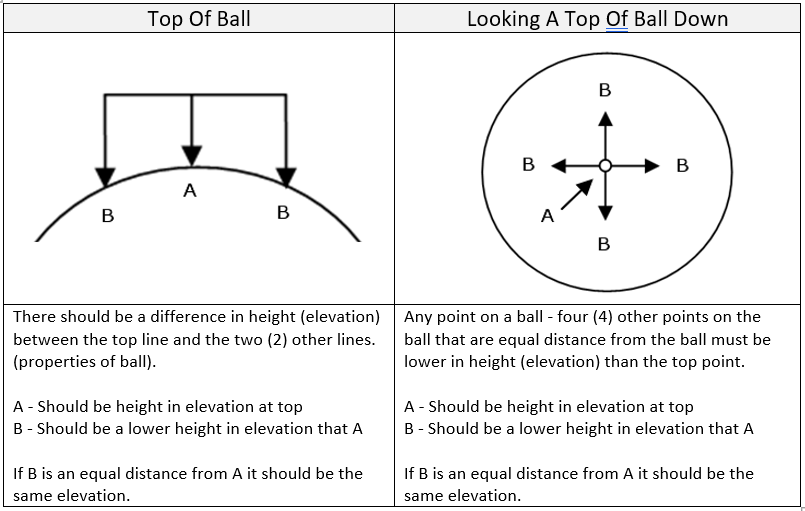
Now we will apply this logic to the curvature of the earth (globe).

Calculations Of The Curvature Of The Earth

There are two (2) measurements of curvature we will use to compare.

First - Rule Of Thumb For Calculating Curvature.( Square Of Distance Multiplied By 8)

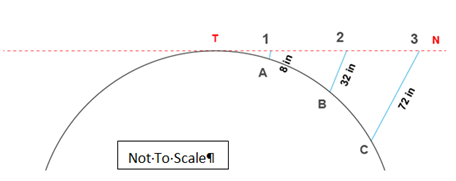
Let the distance from T to figure 1 represent 1 mile, and the fall from 1 to A, 8 inches; then the fall from 2 to B will be 32 inches, and from 3 to C, 72 inches.

In every mile after the first, the curvature downwards from the point T increases as the square of the distance multiplied by 8 inches. The rule, however, requires to be modified after the first thousand miles.

Newtons Principia – Lemma XI - Calculation of Curvature

(Distance squared) / Diameter = Depression.

This is given as a corollary of Lemma XI. In Newton’s Principia. It has nothing to do with us: but is what is necessary if the earth be a globe.

Now, that statement of the law being correct it follows that the square of the Distance, divided by the Diameter equals the Depression. Or:

(Distance) Squared divided by Diameter of Earth

_________ = Depression.
Diameter

If therefore we wish to find the Depression for any given distance we must first square the distance, and divide it by 8,000, (that being the number o f miles in the earth’s diameter).

This will give us the amount of the Depression. The fact that 8 times this particular distance is 64,000, and that the number of inches in one mile is very nearly the same, viz.: 63,360, accounts for the “rule of thumb” which simply multiplies the square of the distance by 8, and reckons the answer as inches.

It will be seen by working out the Distance experimented on in the Bedford Level, how nearly this rough and ready rule corresponds with the exact mathematical calculation. The distance in question is 6 miles.

Now(6 x 6 )
_____ = Depression.
8000

But we cannot divide 36 miles (6 X 6, or 36) by 8,000 without reducing the 36 to some smaller dimension. Let us reduce 36 miles to inches, and then we have

2,280,960 (Six miles) / 8,000
= 285 inches (Depression).

2,280,960 divided by 8,000 = 285 inches

By the rule of thumb method we have

6 x 6 = 36
x 8
______
288

So that by the two methods of calculation, the ‘‘rule of thumb ” method (288 inches) is only 3 inches in excess of the Newtonian mathematical method, which is 285 inches.

Rule Of Thumb - Distance Squared x 8				Newton's Curvature of Earth Calculation
Miles	Kilometers	Curvature Drop Feet	Curvature Drop Meters	Miles	Feet	Inches	Curvature Drop Feet	Curvature Drop Meters
1	0.62	0.67	0.20	1	5,280	63,360	0.66	0.20
2	1.24	2.67	0.81	2	21,120	253,440	2.64	0.80
3	2	6	2	3	47,520	570,240	6	2
4	2	11	3	4	84,480	1,013,760	11	3
5	3	17	5	5	132,000	1,584,000	17	5
6	4	24	7	6	190,080	2,280,960	24	7
7	4	33	10	7	258,720	3,104,640	32	10
8	5	43	13	8	337,920	4,055,040	42	13
9	6	54	16	9	427,680	5,132,160	53	16
10	6	67	20	10	528,000	6,336,000	66	20
20	12	267	81	20	2,112,000	25,344,000	264	80
30	19	600	183	30	4,752,000	57,024,000	594	181
40	25	1,067	325	40	8,448,000	101,376,000	1,056	322
50	31	1,667	508	50	13,200,000	158,400,000	1,650	503
60	37	2,400	732	60	19,008,000	228,096,000	2,376	724
70	43	3,267	996	70	25,872,000	310,464,000	3,234	986
80	50	4,267	1,300	80	33,792,000	405,504,000	4,224	1,287
90	56	5,400	1,646	90	42,768,000	513,216,000	5,346	1,629
100	62	6,667	2,032	100	52,800,000	633,600,000	6,600	2,012
110	68	8,067	2,459	110	63,888,000	766,656,000	7,986	2,434
120	75	9,600	2,926	120	76,032,000	912,384,000	9,504	2,897
130	81	11,267	3,434	130	89,232,000	1,070,784,000	11,154	3,400
140	87	13,067	3,983	140	103,488,000	1,241,856,000	12,936	3,943
150	93	15,000	4,572	150	118,800,000	1,425,600,000	14,850	4,526
160	99	17,067	5,202	160	135,168,000	1,622,016,000	16,896	5,150
170	106	19,267	5,872	170	152,592,000	1,831,104,000	19,074	5,814
180	112	21,600	6,584	180	171,072,000	2,052,864,000	21,384	6,518
190	118	24,067	7,336	190	190,608,000	2,287,296,000	23,826	7,262
200	124	26,667	8,128	200	211,200,000	2,534,400,000	26,400	8,047
210	130	29,400	8,961	210	232,848,000	2,794,176,000	29,106	8,872

Applying The Curvature to The Earth ( Globe, Ball).

If the earth is a globe as we told via modern day science then the earth should have a geographical layout that should follow the rules of a globe.

Remember - we have the following numbers:

Circumference of earth - 24,901 miles divided by 360 degrees equals 69.16 miles

Circumference of earth - 40,075 kilometer divided by 360 degrees equals 111.31 kilometers.

We should be able to take any point on this globe and find the following geographical land mass layout.

Let's do one (1) degree of 360 degrees of 24,901 miles. ( 69.16 miles)

Calculate the curvature we should see via the two (2) models are calculating curvature.

Rule Of Thumb - Distance Squared x 8				Newton's Curvature of Earth Calculation
Miles	Kilometers	Curvature Drop Feet	Curvature Drop Meters	Miles	Feet	Inches	Curvature Drop Feet	Curvature Drop Meters
70	43	3,267	996	70	25,872,000	310,464,000	3,234	986

Ok - applying this to the physical geographical structure of the Earth - show me one place on the entire earth that has this structure. You cannot.

Again - show me one (1) where this is true let alone the entire globe.

One (1) degree - 69.16 miles - the other 4 locations should be physically lower in land mass elevation or 3,267 feet below for rule or thumb or 3,234 feet for Newton's formula.

If the Earth were a globe - then we would see the curvature in the physical geographical structure of the land where we live everywhere.