Best Proof For A Flat Earth – Modern Airplane Travel
Since the beginning of recorded history, man has known that he lives on a flat earth. The Sumerians, Babylon’s, Hebrews, Egyptians, Indians and Chinese all agreed the world did not move and was flat. They saw the sun, moon and the stars moving on the sky.
Heliocentric Model of the Earth
About 500 years ago, new theories were presented that the earth is in fact moving and the sun, moon and stars are all stationary. This began the advent Copernican heliocentric astronomy which has been the dominant theory taught. See Appendix 1 – Heliocentric Model.
500 years ago until this last century, there was no way for anyone to view the earth at 35,000 feet and see the earth’s physical structure. Today – it is a common experience – it is called airplane travel.
Modern Airplane Travel – Last Century
Modern airplane flight has created two (2) new experiences viewed by a significant part of the earth population that we never had until the last century:
• Ability to see the earth’s horizon at 229 miles away from a flight height of 35,000 feet
• Flight speed of 500 – 600 miles per hour.
Physical Sensations
We get into an airplane and feel the thrust of the takeoff and the acceleration and tilting as we ascend at an angle into the sky. We are cautioned not to leave our seats until a cruising level attitude is reached which is normally 35,000 feet. We are usually told by the pilot that we will flying at this level until we reach our destination. Once this level is reached – we are told that we are free to take off our seat belts and move around the cabin. We feel and experience a level flight until we are told that we will be descending into our expected destination. As we descend, we can both see and feel a tilting and descending to ground level.
What We Experience and See
We feel and see the ascent tilt up and the level flight motion when at the proper cruising attitude and the descent tilt down to our destination. We see a level horizon is all directions.
If The Earth Were A Globe – What We Would See And Experience.
If the Earth were a sphere, airplane pilots would have to constantly correct their altitudes downwards so as to not fly straight off into “outer space!”
If the Earth were truly a sphere 25,000 miles circumference curveting 8 inches per mile squared, a pilot wishing to simply maintain their altitude at a typical cruising speed of 500 mph, would have to constantly dip their nose downwards and descend 2,777 feet (over half a mile) every minute! Otherwise, without compensation, in one hour’s time the pilot would find themselves 166,666 feet (31.5 miles) higher than expected!
A plane flying at a typical 35,000 feet wishing to maintain that altitude at the upper-rim of the so-called “Troposphere” in one hour would find themselves over 200,000 feet high into the “Mesosphere” with a steadily raising trajectory the longer they go.
We would experience an ascent to flight height and then a continual descent to correspond with the curvature of the earth. You would definitely feel this and see this as you are moving at 500 – 600 miles per hour.
At 600 Miles per hour – we cover a significant distance on which curvature could be examined. The airplane would need to descend 166,666 feet in the one hour time.
Miles squared x 8 inches of curvature divided by 12 inches per foot. See Appendix 2 – Calculation of Earth Curvature.
((500 x 500) x 8) / 12
500 x 500 x 8 = 2,000,000
2,000,000 /12 = 166,666 feet
View From Within the Plane
What would should see is a very pronounced curvature based on the exact same calculations you would get from the scientists who measure the earth’s calculation. See Appendix 2 – Curvature Calculations.
What you see is flat. But – at 35,000 feet - the horizon is at a distance of 229 miles.
http://www.ringbell.co.uk/info/hdist.htm
Based the standard model for calculating curvature, you should see 34,960 feet lower views on both the ends of your viewing area.
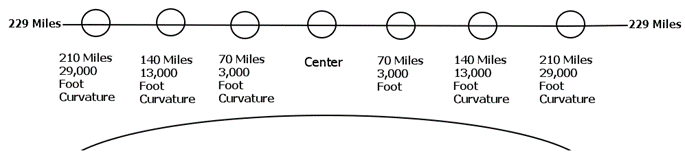
Each 70 miles equals about 1 degree of the 360 degrees of the supposed globe we live on.
At 35,000 feet looking out of an airplane – we will calculate the amount of curvature using the same formula used by professors of Geodesy – Earth science. ( See Appendix 2 – Calculation of Earths Curvature)
Miles squared x 8 inches of curvature divided by 12 inches per foot.
((229 x 229) x 8) / 12
229 x 229 x 8 = 419,528
419,528 /12 = 34,960 feet
The amount of downward curvature would be equal to the height of one of the highest mountains on our planet. I think we could agree that we would be able to see this. Instead – we see flat.
Relative Distances and Curvature
Now the distances traveled you necessitate the pilots make some provision for going around this globe.
If the Earth is 24,900 miles in diameter then if we divided that number by 360 degrees of a sphere we would come up with a distance between each of the 360 degrees of about 70 miles.
I have taken these flights and will attest that my experience was the same on all. Takeoff, ascend to cruising attitude, cruise at that same height for the duration of the flight and descent to the location.
Los Angeles to Rome – Distance – 6,382 miles
6,382 / 70 per degree - 91 degrees traveled – West to East
Los Angeles to Bangkok, Thailand – Distance - 8,309
8,309 / 70 per degree - 118 degrees traveled – East to West
Los Angeles to Capetown, South Africa – Distance – 9,958
9,958 / 70 per degree - 143 degrees traveled – West to East and
South.
Never done personally.
Flight Control Manuals
Flight control manuals assume a Flat earth. They know the earth is flat. They make no provision for the curvature of the earth when they are flying. They ascend and level out and fly to destination and descend. There is no auto pilot that constantly adjusts the level of flight to 35,000.
I have talked to several pilots, and no such compensation for the Earth’s supposed curvature is ever made. When pilots set an altitude, their artificial horizon gauge remains level and so does their course; nothing like the necessary 2,777 foot per minute declination is ever taken into consideration.

Conclusions:
We don’t feel or see a constant declination in an airplane ride that we would need to experience with the curvature of the earth that we are told we have.
We don’t see a curvature on the horizon at 35,000 feet when if the earth were curved we would see a curve down 34,900 feet in our view of the horizon from an airplane – the height of one of the highest locations on earth.
Flight manuals used to teach air navigation to airline pilots uses horizontal plane geometry to calculate their flight plans and makes no provision for the earth’s curvature in their flying.
Ask any pilot – they ascend to their cruising altitude and then fly at that level until they reach their destination. There is no autopilot that constantly adjusts their altitude. If this was happening, you will feel the constant lowering of the flight altitude to the amount of 2,700 feet per minute while in flight.
You have been presented with proof that you have seen with your eyes that the earth is flat on every flight you have ever taken. Based on the curvature calculations presented by Geodesy professors and Isaac Newton’s own method for calculating curvature of the earth, you would see a very different sight when flying at 35,000 feet.
What you do see and feel is true – our eyes are telling the truth – you see flat earth and a horizontal – not curved horizon.
Why we have been told this is another story….
Appendix 1 - Heliocentric Model Of the EarthAppendix 1 - Heliocentric Model Of the Earth
The Heliocentric Model (Earth spins on axis and rotates once per day) is built purely on assumptions that deny all observational and experimental evidence.
Notice these seven assumptions which are indispensable to the Heliocentric Model in general and are so apparent in the Solar Eclipse Phenomena.
1) It must be assumed that the Sun is stationary in the "solar" system relevant to the Earth (and to the Moon) and that it has never traveled East to West daily across the sky as observed by everyone on Earth throughout all history.
2) Likewise, it must be assumed that the Earth rotates West to East ccw (counterclockwise) on an "axis" every 24 hours at an equatorial speed of c. 1040 MPH in spite of there being nothing but a mathematical model's "necessary evidence" for this motion whatsoever.
3) It must be assumed that the Earth is also orbiting the Sun annually (ccw) at an average speed of c. 67,000 MPH.
4) It must be assumed that the Earth’s axial alleged tilt of 23.5 degrees--in combination with its assumed annual orbit around the sun--is the only available scientific explanation for the seasons.
5) The Earth’s atmosphere must be assumed to be just an airy, fixed extension of the alleged rotating Earth. It is assumed and must be assumed that this atmosphere must have the remarkable ability to synchronize speeds of objects in it at all altitudes--birds, clouds, jets, low orbit satellites, alleged geo-synchronous satellites over 22,000 miles out--and to be unaffected by alleged Earth movements of speeds ranging from 1000 MPH to 67,000 MPH to 500,000 MPH to 660,000,000 MPH. This assumption is mandatory once the rotating Earth assumption is made and cannot be ignored in the helio model of the eclipse phenomena.
6) A particularly fantastic assumption necessary to accommodating the precise Solar Eclipse Phenomena in the Helio Mathematical Model involves the bold reversal of the Moon’s observed direction of travel. Acceptance of this. has no basis in reality, of course. Rather, it must be coupled with prior acceptance of the other assumptions of a rotating Earth orbiting a stationary Sun. No moon reversal means no accurate eclipse forecasts and no accurate eclipse forecasts means no heliocentricity model.
7) It must be assumed that the Stars do not move around the Earth diurnally (as they have been observed to do by everyone who has ever lived).
Each one of these seven assumptions is dependent on the other six. They are all interdependent and totally without observational or experimental support. They are solely mathematical models contrived to account for eclipses and other phenomena and replace the fact that what we actually see explains the phenomena.
Appendix 2 - Calculations of the Curvature of the Earth
There are two (2) measurements of curvature we will use to compare.
First - Rule Of Thumb For Calculating Curvature.( Square Of Distance Multiplied By 8)
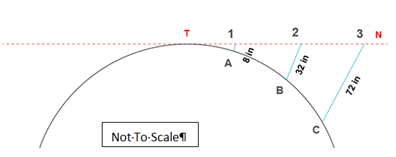
Let the distance from T to figure 1 represent 1 mile, and the fall from 1 to A, 8 inches; then the fall from 2 to B will be 32 inches, and from 3 to C, 72 inches.
In every mile after the first, the curvature downwards from the point T increases as the square of the distance multiplied by 8 inches. The rule, however, requires to be modified after the first thousand miles.
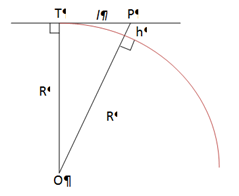
The Pythagorean theorem for triangle TPO => (R+h)2 = R2+l2. So,
h = (R2+l2)0.5 – R
R{[1 +(l/R)2]0.5 -1}
The binomial theorem => (1+x)0.5 = 1 +x/2 –x2/8 +…
Thus, we have h ~ l2/2R, approximately. This shows why your
downward curvature h increases as the square of l, the
distance PT.
The earth surface is close to an ellipsoid and thus the radius
of earth curvature R changes with the latitude of location T.
Near the latitude 45 degrees, R is about 6371 km or 2.0902x107
ft. Using this constant number, you can show that the downward
curvature H is about 8.0025 x L2 inches where L is the
distance PT in (statute) miles.
This formula was given to me by a Professor of Geodesy at Ohio
State University.
Newton’s Principia – Lemma XI - Calculation of Curvature
(Distance squared) / Diameter = Depression.
This is given as a corollary of Lemma XI. In Newton’s Principia. It has nothing to do with us: but is what is necessary if the earth be a globe.
Now, that statement of the law being correct it follows that the square of the Distance, divided by the Diameter equals the Depression. Or:
(Distance) Squared divided by Diameter of Earth
_________ = Depression.
Diameter
If therefore we wish to find the Depression for any given distance we must first square the distance, and divide it by 8,000, (that being the number o f miles in the earth’s diameter).
This will give us the amount of the Depression. The fact that 8 times this particular distance is 64,000, and that the number of inches in one mile is very nearly the same, viz.: 63,360, accounts for the “rule of thumb” which simply multiplies the square of the distance by 8, and reckons the answer as inches.
It will be seen by working out the Distance experimented on in the Bedford Level, how nearly this rough and ready rule corresponds with the exact mathematical calculation. The distance in question is 6 miles.
Now (6 x 6 ) / 8,000 = Depression.
But we cannot divide 36 miles (6 X 6, or 36) by 8,000 without reducing the 36 to some smaller dimension. Let us reduce 36 miles to inches, and then we have
2,280,960 (Six miles) / 8,000
= 285 inches (Depression).
2,280,960 divided by 8,000 = 285 inches
By the rule of thumb method we have
6 x 6 = 36
x 8
______
288
So that by the two methods of calculation, the ‘‘rule of thumb ” method (288 inches) is only 3 inches in excess of the Newtonian mathematical method, which is 285 inches.
|
Rule Of Thumb - Distance Squared x 8 |
|
Newton's Curvature of Earth Calculation |
|||||||
|
Miles |
Kilometers |
Curvature Drop Feet |
Curvature Drop Meters |
|
Miles |
Feet |
Inches |
Curvature Drop Feet |
Curvature Drop Meters |
|
1 |
0.62 |
0.67 |
0.20 |
|
1 |
5,280 |
63,360 |
0.66 |
0.20 |
|
2 |
1.24 |
2.67 |
0.81 |
|
2 |
21,120 |
253,440 |
2.64 |
0.80 |
|
3 |
2 |
6 |
2 |
|
3 |
47,520 |
570,240 |
6 |
2 |
|
4 |
2 |
11 |
3 |
|
4 |
84,480 |
1,013,760 |
11 |
3 |
|
5 |
3 |
17 |
5 |
|
5 |
132,000 |
1,584,000 |
17 |
5 |
|
6 |
4 |
24 |
7 |
|
6 |
190,080 |
2,280,960 |
24 |
7 |
|
7 |
4 |
33 |
10 |
|
7 |
258,720 |
3,104,640 |
32 |
10 |
|
8 |
5 |
43 |
13 |
|
8 |
337,920 |
4,055,040 |
42 |
13 |
|
9 |
6 |
54 |
16 |
|
9 |
427,680 |
5,132,160 |
53 |
16 |
|
10 |
6 |
67 |
20 |
|
10 |
528,000 |
6,336,000 |
66 |
20 |
|
20 |
12 |
267 |
81 |
|
20 |
2,112,000 |
25,344,000 |
264 |
80 |
|
30 |
19 |
600 |
183 |
|
30 |
4,752,000 |
57,024,000 |
594 |
181 |
|
40 |
25 |
1,067 |
325 |
|
40 |
8,448,000 |
101,376,000 |
1,056 |
322 |
|
50 |
31 |
1,667 |
508 |
|
50 |
13,200,000 |
158,400,000 |
1,650 |
503 |
|
60 |
37 |
2,400 |
732 |
|
60 |
19,008,000 |
228,096,000 |
2,376 |
724 |
|
70 |
43 |
3,267 |
996 |
|
70 |
25,872,000 |
310,464,000 |
3,234 |
986 |
|
80 |
50 |
4,267 |
1,300 |
|
80 |
33,792,000 |
405,504,000 |
4,224 |
1,287 |
|
90 |
56 |
5,400 |
1,646 |
|
90 |
42,768,000 |
513,216,000 |
5,346 |
1,629 |
|
100 |
62 |
6,667 |
2,032 |
|
100 |
52,800,000 |
633,600,000 |
6,600 |
2,012 |
|
110 |
68 |
8,067 |
2,459 |
|
110 |
63,888,000 |
766,656,000 |
7,986 |
2,434 |
|
120 |
75 |
9,600 |
2,926 |
|
120 |
76,032,000 |
912,384,000 |
9,504 |
2,897 |
|
130 |
81 |
11,267 |
3,434 |
|
130 |
89,232,000 |
1,070,784,000 |
11,154 |
3,400 |
|
140 |
87 |
13,067 |
3,983 |
|
140 |
103,488,000 |
1,241,856,000 |
12,936 |
3,943 |
|
150 |
93 |
15,000 |
4,572 |
|
150 |
118,800,000 |
1,425,600,000 |
14,850 |
4,526 |
|
160 |
99 |
17,067 |
5,202 |
|
160 |
135,168,000 |
1,622,016,000 |
16,896 |
5,150 |
|
170 |
106 |
19,267 |
5,872 |
|
170 |
152,592,000 |
1,831,104,000 |
19,074 |
5,814 |
|
180 |
112 |
21,600 |
6,584 |
|
180 |
171,072,000 |
2,052,864,000 |
21,384 |
6,518 |
|
190 |
118 |
24,067 |
7,336 |
|
190 |
190,608,000 |
2,287,296,000 |
23,826 |
7,262 |
|
200 |
124 |
26,667 |
8,128 |
|
200 |
211,200,000 |
2,534,400,000 |
26,400 |
8,047 |
|
210 |
130 |
29,400 |
8,961 |
|
210 |
232,848,000 |
2,794,176,000 |
29,106 |
8,872 |
Applying The Curvature to The Earth ( Globe, Ball).
If the earth is a globe as we told via modern day science then the earth should have a geographical layout that should follow the rules of a globe.
Remember - we have the following numbers:
Circumference of earth - 24,901 miles divided by 360 degrees equals 69.16 miles
Circumference of earth - 40,075 kilometer divided by 360 degrees equals 111.31 kilometers.
We should be able to take any point on this globe and find the following geographical land mass layout.
Let's do one (1) degree of 360 degrees of 24,901 miles. ( 69.16 miles)
Calculate the curvature we should see via the two (2) models are calculating curvature.
|
Rule Of Thumb - Distance Squared x 8 |
|
Newton's Curvature of Earth Calculation |
|||||||
|
Miles |
Kilometers |
Curvature Drop Feet |
Curvature Drop Meters |
|
Miles |
Feet |
Inches |
Curvature Drop Feet |
Curvature Drop Meters |
|
70 |
43 |
3,267 |
996 |
|
70 |
25,872,000 |
310,464,000 |
3,234 |
986 |
Ok - applying this to the physical geographical structure of the Earth - show me one place on the entire earth that has this structure. You cannot.
If the Earth is a true globe – there wouldn’t be a single serious argument against the fact of the Earth’s globular shape (roundness) ….Not a single argument!
There would be no flat earth arguments as the earth would display the characteristics of a globe and flatearthers would not be able to present any arguments as to flatness or lack of globularity of the earth.
A search of the circumference of the earth on Google will show the following:
The earth is 24,901 miles (40,075 kilometers) around. This means if you start at the center of the equator and travel around the earth you will return to the same place and travel 24,901 miles.

Now - since the earth is presented as a globe - a ball - you should be able to break this circle into 360 degrees as all circles (balls) can be divided into 360 parts.
Circumference of earth - 24,901 miles divided by 360 degrees equals 69.16 miles
Circumference of earth - 40,075 kilometer divided by 360 degrees equals 111.31 kilometers.
All we have done is create a division of how much space would be between each of these 360 degrees.
So - every 69.16 miles or 111.31 km we have a division which equals one degree of the total 360 degrees of a circle.
Now - let’s look at a ball ( globe) and compare the distance between these two (2) points.
If we take any point on a ball and move an equal distance from that point in 4 directions we will find the first position will be the top and the other four (4) distances will be lower in orientation to the first point.
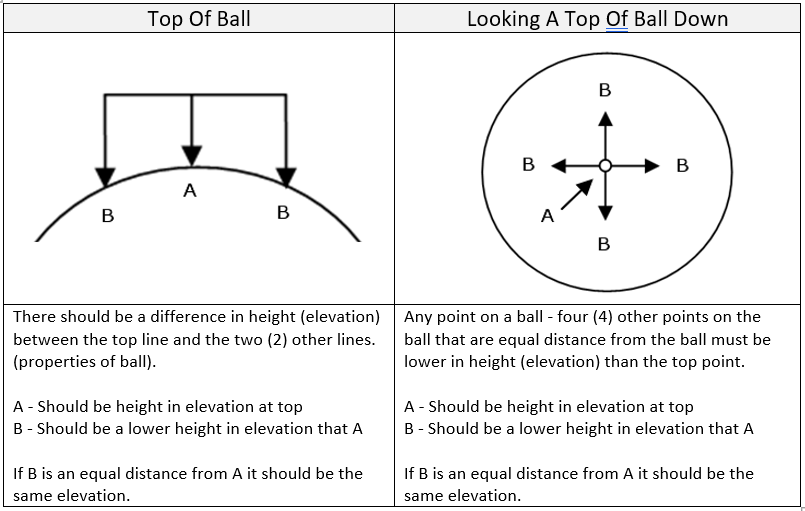
Now we will apply this logic to the curvature of the earth (globe).
Again - show me one (1) where this is true let alone the entire globe.
One (1) degree - 69.16 miles - the other 4 locations should be physically lower in land mass elevation or 3,267 feet below for rule of thumb or 3,234 feet for Newton's formula.
If the Earth were a globe - then we would see the curvature in the physical geographical structure of the land where we live everywhere.